The invlib Library
invlib is a C++ template library that implements Bayesian methods for inverse problems in remote sensing. I developed invlib as part of my Master’s thesis work at the department Earth and Space Sciences at Chalmers University of Technology.
This project evolved from my work as a student research assistant working on integrating retrieval functionality into the ARTS package. My primary aim was to extend and generalize this first implementation making it a highly configurable and generally applicable library for remote sensing data retrieval.
Inverse Problems in Remote Sensing
Remote sensing denotes the acquisition of information about a certain physical system remotely, as opposed to obtaining this information directly through an in-situ measurement. Due to their ability to deliver continuous observations on a global scale, remote sensing and in particular satellite remote sensing are important observational techniques in earth and climate science. Remote sensing techniques generally use electromagnetic radiation transmitted through or reflected by a physical system to measure its properties. The data that is acquired by remote sensing instruments usually consists of one or several spectra of electromagnetic radiation. The task of inferring physically relevant information from this data is called data retrieval. Figure 1 displays an example of how the data recorded by such a satellite may look. Displayed in the plot are electromagnetic spectra that have been recorded by the Odin SMR. As will be shown below, using sophisticated data processing, it is possible to reconstruct the 2-dimensional water vapor and temperature distribution of the atmosphere.

Figure 1: Electromagnetic spectra recorded by the Odin SMR.
Mathematically, the data retrieval is an inverse problem: The spectra recorded by the detector are the results of the interaction of the electromagnetic radiation with the system under investigation. This process is called the forward problem and can usually be computed relatively easily. The aim of the data retrieval is to invert this process in order find the state of the system that lead to the recorded spectra.
Mathematical Formulation
Below I will briefly present the underlying mathematical formulation of the data retrieval. I include this presentation for completeness, if you are not interested in the mathematical details or familiar with the OEM may skip this section.
The method used for the data retrieval is known as the Optimal Estimator Method (OEM) as described in [2] or more generally as the maximum a posteriori estimator of the posterior distribution as described in [3].
Using a Bayesian approach, the data retrieval problem can be formulated as follows: Assume we are observing a system described by a parameter vector \(\mathbf{x} \in \mathbb{R}^n\). The observations \(\mathbf{y} \in \mathbb{R}^m\) are the result of a physical process that is described by a conditional probability distribution \(P(\mathbf{y}\:|\:\mathbf{x})\). In particular here it is assumed that \(P(\mathbf{y}\:|\:\mathbf{x})\) is multivariate Gaussian
\begin{align} P(\mathbf{y}\: |\: \mathbf{x}) = \frac{1}{(2\pi)^\frac{m}{2}|\mathbf{S}_\epsilon |^{\frac{1}{2}}} \exp \left \{- \frac{1}{2}(K(\mathbf{x}) - \mathbf{y})^T \mathbf{S}_\epsilon^{-1} (K(\mathbf{x}) - \mathbf{y}) \right \} \end{align}with mean \(F(\mathbf{x})\) and covariance matrix \(\mathbf{S}_\epsilon\). The mean \(F(\mathbf{x})\) is given by the forward model \(F : \mathbb{R}^n \to \mathbb{R}^m\), which describes the propagation of the radiation and the process of its detection. The knowledge available about the system before the measurement has been performed is also assumed to be Gaussian with mean given by the a priori state \(\mathbf{x}_a\) and covariance matrix \(\mathbf{S}_a\). Applying Bayes Theorem, the general solution of the inverse problem is obtained as the a posteriori distribution \(P(\mathbf{x} \:|\: \mathbf{y})\):
\begin{align} P(\mathbf{x}\:|\:\mathbf{y}) & \propto \exp \left \{-\frac{1}{2} \left ( (\mathbf{y} - F(\mathbf{x}))^T \mathbf{S}_{\epsilon}^{-1} (\mathbf{y} - F(\mathbf{x})) + (\mathbf{x} - \mathbf{x}_a)^T\mathbf{S}_a^{-1}(\mathbf{x} - \mathbf{x}_a) \right ) \right \} \end{align}Only in very special cases, for example when the forward model \(F\) is linear, the aposteriori distribution can be expressed in closed form. The general approach is to compute the most likely state of the system, also called the maximum a posteriori (MAP) state as well as a suitable uncertainty measure. The MAP state can be found by minimizing the negative log likelihood
\begin{align} \mathcal{L}(\mathbf{x}) \propto (F(\mathbf{x}) - \mathbf{y}) \mathbf{S}_{\epsilon}^{-1} (F(\mathbf{x}) - \mathbf{y}) + (\mathbf{x} - \mathbf{x}_a) \mathbf{S}_{a}^{-1} (\mathbf{x} - \mathbf{x}_a) \end{align}Implementation
invlib has been developed with the aim of providing functionality for the computation of MAP estimators and corresponding uncertainty measures for inverse problems of the form described above. In particular invlib aims to:
- Conserve the generality of the mathematical formulation, making it suitable for a large range of inverse problems.
- Be sufficiently efficient to handle also large retrieval problems.
invlib is written conforming to the C++11 standard. It uses template programming to implement generic solvers for the computation of MAP estimators. The library is freely available online and published under the MIT license.
Features
So far, the main features provided by invlib are:
- Three formulations of MAP estimators for Gaussian inverse problems.
- Generic implementations of Gauss-Newton and Levenberg-Marquardt algorithms for minimization of the log likelihood.
- A generic implementation of the conjugate gradient method to be used as a solver for the linear subproblem of the optimization method.
- Generic MPI matrix and vector types to perform calculations on distributed computing systems.
In addition to that, invlib implements a generic, optimized matrix algebra that simplifies the implementation of custom computations and separates their formulation from the underlying implementation of the data types.
Science Usecases
To test the invlib library and demonstrate its capabilities, two retrievals with data from two different satellite missions have been performed: The Odin SMR mission and the future MATS mission.
Tomographic Retrievals of Odin SMR Data
The Odin SMR records submillimetre radiation emitted by water molecules in a backwards-looking limb sounding geometry. This means, the SMR is directed backwards along the satellite orbit and records radiation along lines of sight that are tangential to the atmosphere. While the satellite moves along its orbit, the antenna moves up and down, scanning heights between 75 and 90 km. The viewing geometry is illustrated in the figure below.

Figure 2: Odin SMR viewing geometry.
Due to the overlap of the lines of sight, tomographic techniques can be applied. These allow for the data to be retrieved in 2D with an increased resolution. The retrievals have been performed using data recorded over half an orbit of the satellite. Figure 1 displays the spectra from the first sweep over the viewing angles of the instrument used for the retrievals. The retrieved atmospheric quantities are water vapor and temperature.
The a priori water vapor concentrations and the retrieved water vapor concentrations are displayed in the figure below. The most interesting features of the water vapor distribution are the peaks located at \(70^\circ, 80^\circ\) and \(110^\circ\) along orbit. These are related to the formation of polar mesospheric clouds, whose study is the main objective of these observations.
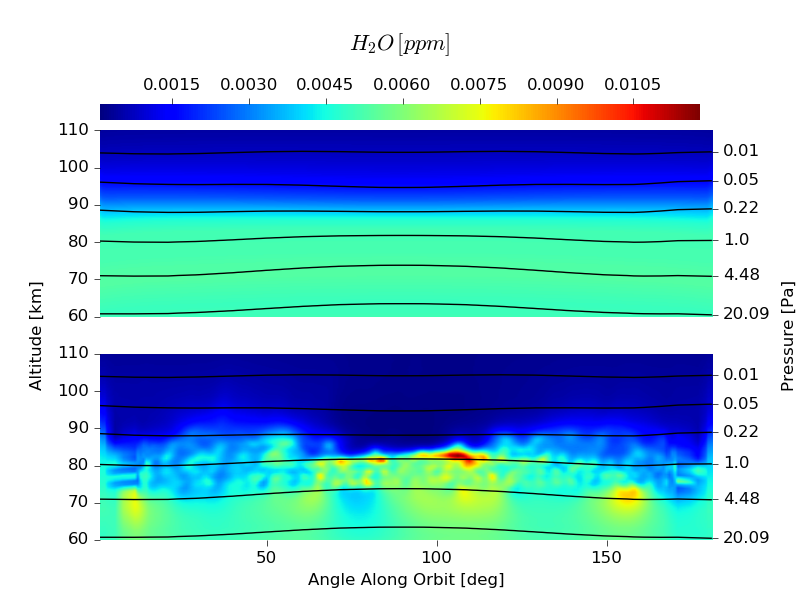
Figure 3: A priori and retrieved water vapor concentrations obtained from the data displayed in Figure 1
In addition to the water vapor concentrations, also the temperature has been retrieved. From the results displayed in the plot below it can be seen that the temperature of the Mesopause is lowest at the poles, which is due to the mesospheric overturning circulation.

Figure 4: A priori and retrieved temperature obtained from the data displayed in Figure 1
These retrievals have first been performed by Christensen et al. in [1] With the newly developed retrieval implementation it was for the first time possible to perform the retrieval for a complete orbit within a single computation. Before, each half-orbit had to be distributed into overlapping chunks due to memory limitations. Furthermore, using invlibs distributed data types, the computations could be further sped up, as displayed in the figure below.

Figure 5: Compute time for the distributed retrievals of Odin SMR data.
Tomographic Retrieval of Simulated MATS Data
In order to demonstrate the usefulness of the invlib library also outside of ARTS, retrievals of simulated data from the future MATS satellite mission have been performed.
The Mesospheric Airglow/Aerosol Tomography and Spectroscopy (MATS) satellite mission is planned to be launched in 2018 and will use optical measurement techniques to study the mesosphere. The MATS satellite measures optical emission from the upper mesosphere and can be used to perform 3D retrievals of the scattering coefficient of the atmosphere. The measurements used for this retrieval are simulated data of an atmospheric volume containing a PMC. A volume rendering of the retrieved three-dimensional volume is displayed in the animation below.

Figure 6: Retrieved scattering coefficient for simulated measurements from the MATS satellite mission.
For this retrieval implementation the Eigen 3 library has been used for the underlying matrix and vector types. Also here it was possible to speed up the retrieval by parallelizing the computations using invlibs generic distributed matrix types.

Figure 7: Computing time of the MATS retrieval with respect to number of parallel processes.
Acknowledgements
First of all I would like to thank my supervisor Patrick Eriksson for introducing me to the very exciting topic of remote sensing data retrieval and the opportunity to work on this project as well as his help and guidance during the work on this thesis project. I also want to thank Ole Martin Christensen for providing the data for the Odin SMR as well as the MATS retrieval. Furthermore I want to thank Dr. Jörn Ungermann for a very fruitful discussion on remote sensing data retrieval.
The computations presented in this thesis were performed on resources at Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC).
Bibliography
[1] O.M. Christensen, P. Eriksson, J. Urban, D.P. Murtagh, K. Hultgren, J. Gumbel, Tomographic retrieval of water vapour and temperature around polar mesospheric clouds using odin-sMR, Atmospheric Measurement Techniques. 8 (2015) 1981–1999.
[2] C.D. Rodgers, Inverse methods for atmospheric sounding: Theory and practice, World Scientific, 2000.
[3] A. Tarantola, Inverse problem theory and methods for model parameter estimation, SIAM, Philadelphia, 2005.