Fast, Approximate Exponential Function in C++

Recently, I was working on implementing a remote sensing retrieval that required computing a large number Gaussian probabilities. The required evaluation of the exponential function was in this case critical for the compute time of the method. Since the retrieval method itself was only an appoximation, I started looking into whether some accuracy could be exchanged against performance. Since a quick search on the internet didn’t yield a satisfactory solution that was open and portable, I ended up writing a small C++ template library (fastexp) that implements two approximations of the exponential function in a portable and efficient way. In this post, I will describe the two approximations, their implementations and some performance results.

Key findings

• The exponential function from the gcc standard library can do quite a good job if compiled with the following compiler flags:

g++ -O3 -ffast-math -funsafe-math-optimizations -msse4.2

• If accuracy is not a primary concern, the calculation of the exponential function can be sped up by a factor of 4 or 7 depending on whether single or double precision arithmetic is used.

• A small C++ template library providing portable implementations of two approximations of the exponential function supporting vectorization been developed and is available here.

Approximating the exponential function

Two different ways of computing approximations of the exponential function are considered here. The first one is a mathematical approximation based on the definition of the exponential function as an infinite product. The second one is way cooler more technical and exploits the format in which IEEE 754 floating point numbers are defined.

The truncated product approximation

The exponential function can be defined as an infinite product:

\[ \exp(x) = \lim_{n \to \infty}\left (1 + \frac{x}{n} \right)^n \]

Hence, an approximation of the exponential function can be obtained by evaluating the product for a fixed value \(n = m\):

\[ \exp(x) \approx \left (1 + \frac{x}{m} \right )^m \]

This exponentiation in the equation above can be implemented efficiently by applying exponentiation by squaring. Using C++ templates and turning the exponentiation loop into a compile time loop, a flexible implementation that also generates efficient code can be obtained:

template<typename Real, size_t degree, size_t i = 0>
    struct Recursion {
        static Real evaluate(Real x) {
            constexpr Real c = 1.0 / static_cast<Real>(1u << degree);
            x = Recursion<Real, degree, i + 1>::evaluate(x);
            return x * x;
        }
    };

template<typename Real, size_t degree>
    struct Recursion<Real, degree, degree> {
    static Real evaluate(Real x) {
        constexpr Real c = 1.0 / static_cast<Real>(1u << degree);
        x = 1.0 + c * x;
        return x;
    }
};

As an example, compiling the following executable with the -O3 flag

int main(int argc, const char **argv) {
    double x = Recursion<double, 8>::evaluate(atof(argv[1]));
    std::cout << x << std::endl;
}

yields the following assembler code:

...
mulsd   .LC0(%rip), %xmm0
movl    $_ZSt4cout, %edi
addsd   .LC1(%rip), %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
mulsd   %xmm0, %xmm0
...

Except the movl expression in the second line, which is related to the output of the results, the assembler code contains the minimum of instruction required to compute the approximate exponential.

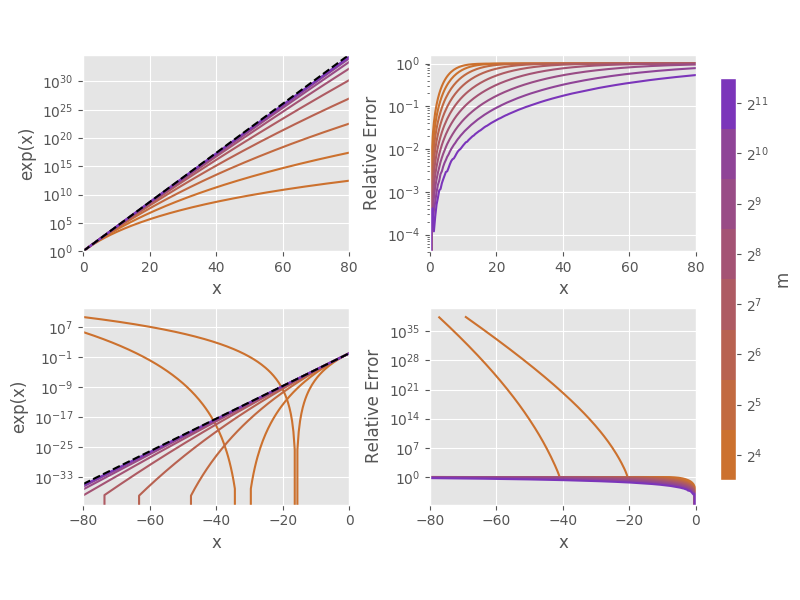
A plot of the approximation functions is given in the figure below. The degree from the function definition translates to a truncation threshold of \(m = 2^\text{degree}\). Below the approximations are given for \(m = 2^4, \ldots, 2^{12}\). The plots illustrates important properties of the approximation:

• The approximation is best for small \(x\) but deviates considerably for large \(x\).
• For positive \(x\) the approximation is bounded above by the true exponential function.
• For negative \(x\) the same holds up to a value of \(-m\) after which the absolute value of the approximation function increases again, leading to even larger errors.

Approximate exponential using IEEE 754 manipulation

The second approximation considered here exploits the definition of the IEEE 754 floating point format. To my best knowledge this was first proposed by Schraudolph in [2]. The implementation presented here also uses the idea proposed by Malossi et al. in [1] to improve the approximation using a polynomial fit to the error function.

The way the approximation works is based on the fact that a number y in IEEE 754 floating point format is represented in the form \[ y = (1.0 + m) \cdot 2^{e}. \] Of the bits in memory that represent the number \(y\), a certain range is holds the mantissa \(m\) and another the exponent \(e\). Hence, given a binary representation of an integer \(x_i\), the 2-exponential \(y = 2^x\) can be computed simply by copying the bits representing \(x_i\) into the exponent bits of \(y\). This is illustrated for a hypothetical 8-bit floating point type in the graphic below. The blue bits represent the exponent bits of the floating point format and the purple ones the mantissa bits. The first bit is a sign bit which we don’t care about here.

If \(x\) is a floating point number, things get a bit more tricky. Using \(x_i\) and \(x_f\) to denote the integer and fractional part of \(x = x_i + x_f\), one can write

\[ 2^x = 2^{x_i} \cdot 2^{x_f} = (1.0 + \mathcal{K}(x_f)) \cdot 2^{x_i}, \]

where \(\mathcal{K}(x_f)\) is a correction function that interpolates between the integer exponentials \(2^{x_i}\) and \(2^{x_i + 1}\). The exact form of the correction form is given by \[ \mathcal{K}(x_f) = 2^{x_f} - 1.0. \]

If there was an efficient way of computing \(\mathcal{K}(x_f)\) for values \(x_f \in [0, 1]\), it would be possible to compute the exact value of the exponential function. However, since this is not the case, \(\mathcal{K}\) is approximated using a polynomial fit. The choice of the degree of the polynomial fit determines how well the exponential function is approximated and how much operations are necessary to approximate the exponential.

The left panels in the figure below show plots of the approximate (colored, solid) and the true exponential function (black, dashed). Note that the approximation errors are actually so small, that the true exponential lies directly above the approximate curves. The relative approximation error with respect to the true exponential function is displayed in the right panels. Compared to the relative errors of the truncated product approximation given above, it is obvious that this approximation method provides much smaller errors over the complete range of values considered. Moreover, with a polynomial fit of degree five, the approximation has almost recovered machine precision for single precision arithmetic.

A function template implementing the approximation is given below. Some additional code that takes care of the polynomial fit as well as class templates holding the fit coefficients was omitted, but this should show the most important parts. The full implementation can be found here. In short, what the function does is the following:

• Multiply \(x\) by \(\log_2(e)\) (Since we’re computing \(2^{\log_2(e) x}\) rather than \(\exp\{x\}\))
• Evaluate the polynomial fit of the error function \(k = \mathcal{K(x_f)}\)
• Write \(k + 1\) into e to set the exponent to 0 and the mantissa to \(k\)
• Convert \(x_i\) to an integer and write the result into the exponent of e

template<typename Real, size_t degree>
struct IEEE {
    static Real evaluate(Real x) {
        using unsigned_t = typename Info<Real>::unsigned_t;
        constexpr unsigned_t shift = static_cast<unsigned_t>(1) << Info<Real>::shift;

        x *= Info<Real>::log2e;
        Real xi = floor(x);
        Real xf = x - xi;

        Real k = PolynomialFit<Real, degree, 0>::evaluate(xf) + 1.0;
        unsigned_t e = reinterpret_cast<const unsigned_t &>(k);
        e += shift * static_cast<unsigned_t>(xi);
        return reinterpret_cast<Real &>(e);
    }
};

Performance

In this section, the performance of the two approximate exponential functions is evaluated and compared to the standard implementations.

The benchmark scenario is the application of the exponential function to a large array of \(10^8\) elements. The results shown here were obtained on an Intel Core i7-2640M CPU (2.80GHz) CPU. Only single core performance is considered, since the optimizations presented here are unrelated to parallelization.

Vectorized exponential

In order to obtain good single core performance it is essential to exploit SIMD capabilities of the CPU. OpenMP is used here to ensure vectorization of the loop over the array. The function given below is the function that is used for the benchmark. It implements a generic, vectorized vector exponential, that allows the user to choose approximation method and the degree of the approximation.

template
<
typename Real,
template<typename, size_t> typename Approximation = IEEE,
size_t degree = 2
>
inline void exp(Real *x, size_t n) {
    // Vectorized part.
    #pragma omp simd
    for (size_t i = 0; i < n; ++i) {
        Real e = fastexp::exp<Real, Approximation, degree>(x[i]);
        x[i] = e;
    }
}

Compilers

The tests below are performed using gcc 7.1.0, icc 18.0.2 and clang++ 6.0.0. However, I am not an expert using icc and clang++ so there might be optimization flags that I am missing. The main purpose of the comparison here is to ensure that switching to another compiler doesn’t give much better performance right away.

For compilation with gcc the following flags were used:

 -march=native -mtune=native -O3 -ffast-math -funsafe-math-optimizations -fopenmp

For the intel compiler only -fast and the -qopenmp options are used, which is equivalent to

 -xHOST -O3 -ipo -no-prec-div -static -fp-model fast=2 -qopenmp.

For compilation with clang, the following flags have been used

-std=c++11 -stdlib=libc++ -Ofast -Rpass=loop-vectorize

Single precision

The timing results for single precision arithmetic are given below. The GNU compiler did the best job in optimizing the approximate exponential functions. Runtimes of the considered functions slightly outperform the Intel compiler, followed by the Clang compiler. On the contrary, the Intel compiler yields by far the best performance for the standard exponential outperforming the other two compilers by an order of magnitude. However, for the GNU compiler the compute time can be reduced by a factor of 10 if instead of -march=native the instruction set was set explicitly to -msse4.2. Setting the instruction set explicitly reduced the compute time for the benchmark from \(\sim5000\:ms\) to \(449\: ms\).

Double precision

For double precision arithmetic, the results look slightly different. The difference in compute times for the approximate exponential functions is reduced. The Intel and GNU compiler perform approximately equally well followed by Clang. The GNU standard implementation does a considerably better job here but is still outperformed by the Intel implementation. The Clang compiler yields the slowest standard implementation.

Summary and conclusions

The original motivation for this investigation was the bad performance of the GNU standard library implementation of the exponential function for single precision arithmetic that has also been observed here. However, as discovered during the development of this project, the compute time can be reduced considerably if the instruction set flag is set correctly. The disadvantage with setting the instruction set explicitly is that the compilation isn’t portable anymore.

The C++ library that has been developed performs well over all considered compilers, which indicates that it generates efficient code and does so without resorting to vector intrinsics or other non-portable optimzations. The implementation makes use of C++ templates, which allow the user to choose the approximation type and degree. The use of templates also has the advantage that only templates that are instantiated in the code are compiled and included in the executable, which avoids code bloat.

For the GNU compiler, which I am mainly using currently, considerable gains in performance can be achieved for single precision arithmetic. This is the use case that I was mainly interested in and here the fastexp implementation should be able to improve performance. In general, applications that require only an approximate value of the exponential function or require the evaluation only for small arguments should be able to profit from this implementation. It should be noted however that the implementation presented here doesn’t include safeguards for cases when the argument of the exponential becomes too large, which should therefore be checked if the range can not be limited a priori.

Bibliography